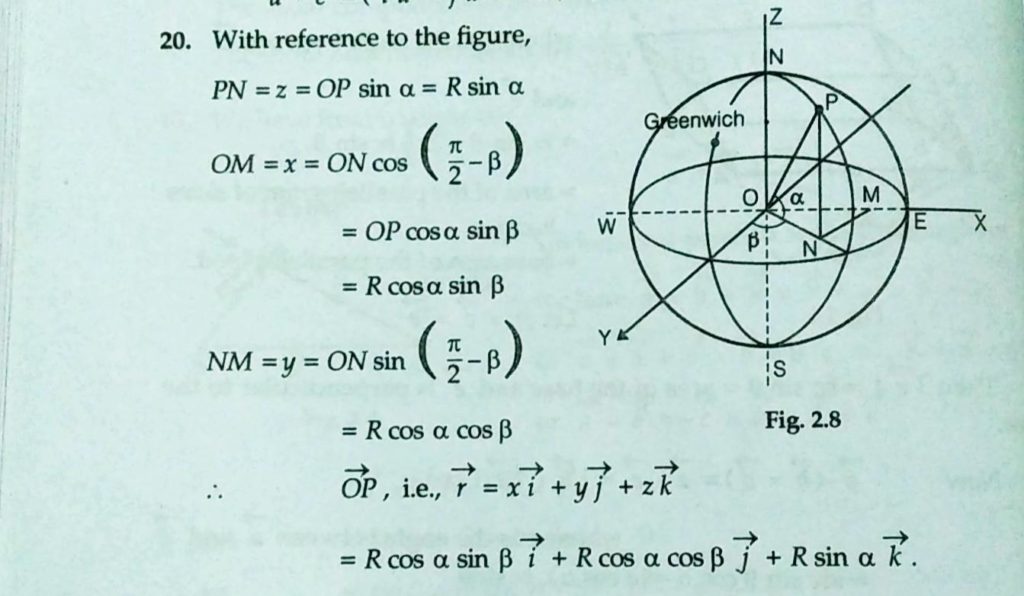
Show that the position vector of a place on the surface of the earth with latitude and longitude α∘N and β∘E respectively, is r→ = R cos α sin βiˆ+ R cos α cos βjˆ+ R sin α kˆ, where R is the radius of the earth.The frame of reference is erected at the centre of the earth with the polar radius as the z-axis and the intersection of the equatorial plane and the meridian plane through Greenwich as the y-axis.