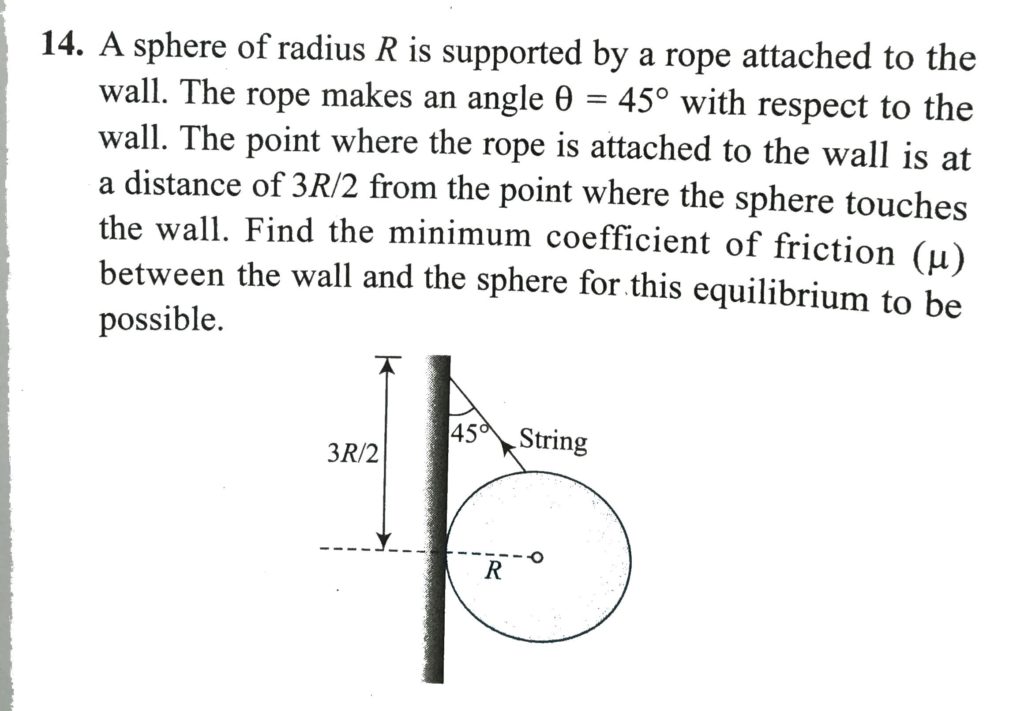
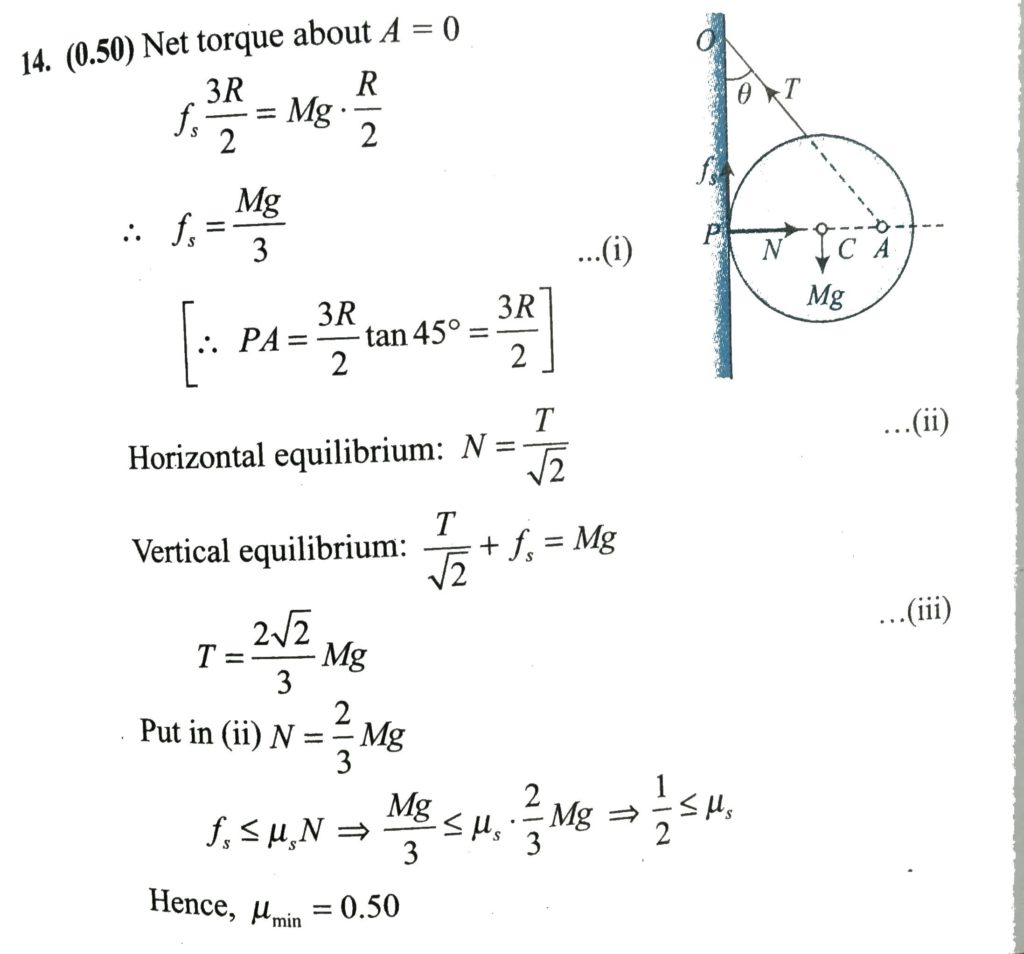
A sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.