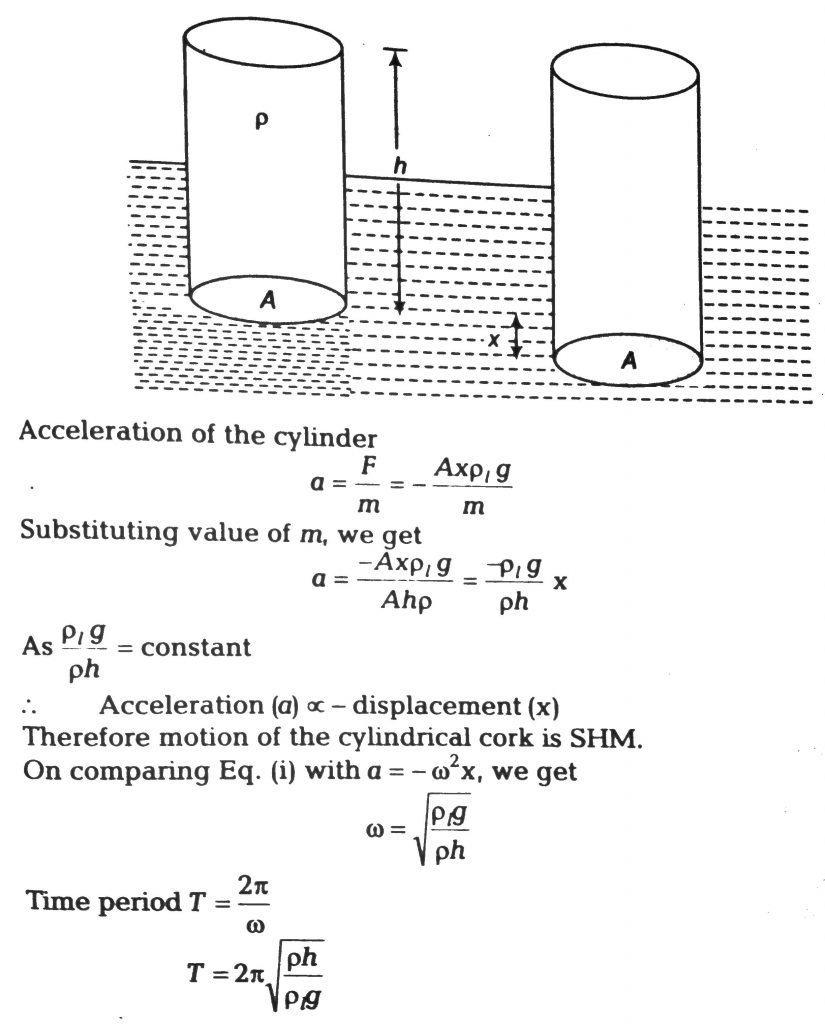
A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T = 2π hρ/ρ1g−−−−√ where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).